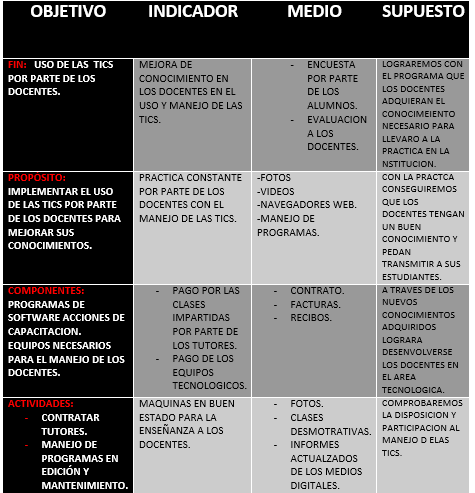
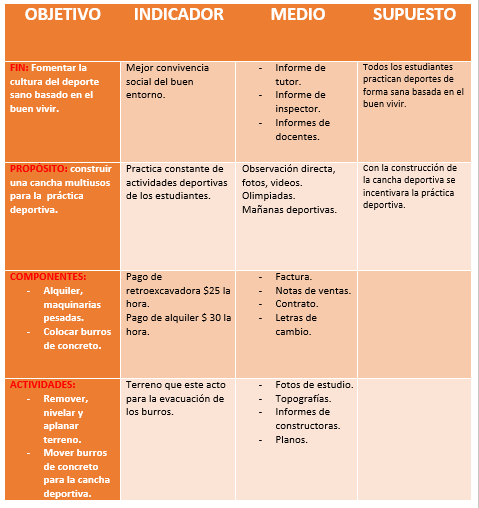
Los términos “dependiente” e “independiente”:
Se utilizan para
representar una relación de “causalidad” entre dos variables. La relación es la
siguiente: el valor de la variable dependiente ‘depende’ del valor de la
variable independiente. En otras palabras: la variable independiente determina,
en alguna medida (medida que puede ser mayor o menor), el valor de la variable
dependiente. Utilizando otros términos, la variable independiente “causa” la variable
dependiente. O sea que el comportamiento de la variable dependiente se podría
predecir sobre la base del comportamiento de la variable independiente.
Por ejemplo,
consideremos la siguiente hipótesis: un buen maestro causa que los estudiantes
aprendan. En este caso, “buen maestro” es la variable independiente, mientras
que “grado de aprendizaje” (de los estudiantes) es la variable dependiente.
Pero no siempre es fácil, o ni siquiera posible, saber cuál es la variable
dependiente y cuál la independiente en una relación. Siguiendo con el ejemplo
anterior, ¿es cierto que el aprendizaje de los niños resulta de la calidad del
maestro? Por ejemplo, ¿el hecho de que los estudiantes de la escuela A tengan
un mejor rendimiento que los de la escuela B significa que los maestros de la
escuela A son mejores que los de la escuela B? Para empezar, quizás los
estudiantes de la escuela A son más aventajados en cierto respecto, o hay otros
elementos que causan ese mayor aprendizaje que no tienen nada que ver con los maestros.
El problema
de la determinación de causalidad (¿cuáles variables son dependientes y cuáles
independientes?) es uno de los problemas más serios que enfrenta la
estadística. El análisis empírico o estadístico sólo puede decirnos si dos
variables parecen estar relacionadas, pero no puede decirnos: (a) si de hecho
existe una relación de dependencia y (b) cuál es la dirección de dicha relación
(cuál es la “causa” y cuál el efecto o la variable “causada”). Necesitamos una
“teoría” para dar plausibilidad a una relación empírica.
Considere la
siguiente cuestión: ¿Es el aumento del ingreso per capita de un país que causa
mejoras en el nivel de educación o la mejora en el nivel de educación que causa
mejoras en el ingreso pr capita? ¿O tal vez un tercer factor es la causa de
ambos? ¿Cultura? Este complejo y viejo debate no se puede resolver sólo sobre
la base del análisis estadístico, aunque la estadística es un importante
instrumento en nuestros continuos esfuerzos por dilucidar estas cuestiones. El
debate mencionado ha persistido por décadas, además, porque muchas de las
teorías que han sido propuestas para explicar la relación entre educación y
desarrollo económico no pueden ser refutadas sólo sobre la base del análisis
empírico.
Vayamos por
un momento al tema de la interpretación de gráficos (tratado en mayor detalle
en los módulos 3 y 4 de esta guía). Un gráfico representa una relación entre
por lo menos dos variables. En matemáticas y geometría, la variable dependiente
se denomina X y se representa en el eje horizontal del gráfico, mientras que la
variable independiente se llama Y (o ‘independiente’, para facilitar la
memorización) y se representa en el eje vertical. En la Figura 1, a
continuación, se muestra un ejemplo de una “curva de oferta” que presenta la
relación entre dos variables: el salario de los maestros y la cantidad o número
de maestros disponibles o que ofrecen sus servicios.